What is section modulus?
Section modulus is a geometric property used in engineering and structural design to quantify a section’s ability to resist bending or flexural deformation. It is particularly important in the design of beams and other structural elements subject to bending moments.
The section modulus (denoted as “S”) is calculated based on the shape and dimensions of a cross-sectional area. It represents the distribution of material around the neutral axis, which is a line or plane within the section where there is no bending stress during deformation.
For a given cross-sectional shape, the formula for calculating the section modulus can vary. Here are the general formulas for common shapes:
- Rectangular Section: �=�⋅�26S=6b⋅d2 where �b is the width of the rectangular section, and �d is the depth.
- Circular Section: �=�⋅�332S=32π⋅D3 where �D is the diameter of the circular section.
- I-Beam Section: �=16⋅�⋅ℎ2S=61⋅b⋅h2 where �b is the width of the flange, and ℎh is the height of the web.
The unit of section modulus is typically length cubed (e.g., mm3,in3mm3,in3).
The section modulus is a crucial parameter in structural engineering because it helps engineers understand how different shapes distribute material to resist bending moments. Sections with larger section moduli are generally more effective in resisting bending and are preferred in structural design. Engineers use section modulus calculations to assess the strength and stability of structural components, ensuring they meet safety and performance requirements.
Section modulus is a geometric property of a cross-sectional shape. It’s used to determine the strength and stiffness of
Section modulus is also the ratio of the total
resisted by the section to the stress in the extreme fiber. This is equal to yield stress.
Section modulus is a measure of a beam’s ability to resist bending stress. A beam with a higher section modulus will be able to withstand greater bending stress without failing.
Section modulus is denoted by the letter S For example, in a circle, the largest distance equals the radius, while it equals half the height in a rectangle.
Section modulus is a geometric property for a given cross-section used in the design of beams or flexural members. Other geometric properties used in design include area for tension and shear, radius of gyration for compression, and moment of inertia and polar moment of inertia for stiffness.
Another property used in beam design is section modulus (Z).
The section modulus of the cross-sectional shape is of significant importance in designing beams. It is a direct measure of the strength of the beam. A beam that has a larger section modulus than another will be stronger and capable of supporting greater loads.
It includes the idea that most of the work in bending is being done by the extreme fibres of the beam, ie the top and bottom fibres of the section. The distance of the fibres from top to bottom is therefore built into the calculation.
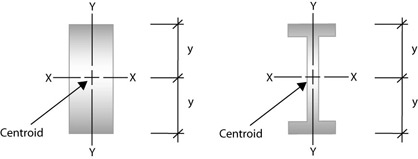
The elastic modulus is denoted by Z. To calculate Z, the distance (y) to the extreme fibres from the centroid (or neutral axis) must be found as that is where the maximum stress could cause failure.
It is known that the stress in a fibre is proportional to its distance from the neutral axis. If y max is the distance of the extreme fibre from neutral axis then. Here, Z represents Section modulus or Modulus of section, i.e., Z = I / y max. Thus, moment of resistance of a section is. M = f z = p z.
What is the section modulus (Z) for a rectangular section? Explanation: The modulus of section may be defined as the ratio of moment of inertia to the distance to the extreme fibre. It is denoted by Z. Z= I/y ; For rectangular section, I = bd3/12 & y = d/2.
Theory:
The ratio of Area Moment of Inertia to the Distance from the Neutral Axis to the Point where the Bending Normal Stress is determined.
Section modulus (Z) = I/Y
In Detail:
It is a geometric property for a given cross-section used in the design of beams or flexural members.
Also, it is the direct Measure of Strength of a beam. Higher the Section Modulus higher will be the Resistance to Bending.
The property used in beam design is section modulus (Z).
It is the ratio of moment of inertia about the neutral axis upon the farthest point of a section from the neutral axis.
A beam that has a larger section modulus than another will be stronger and capable of supporting greater loads, it is denoted by Z.
To calculate Z, the distance (y) to the extreme fibres from the centroid (or neutral axis) must be found as that is where the maximum stress could cause failure.
Z = I/Y(max)
Hence, if the maximum stress offered by the section is known we can easily compute the moment of resistance that can be offered by the section. hence for a beam of given material the greatest moment of resistance the beam section can offer is given by
M = f(safe).Z
where, f(safe) = maximum bending stress which occurs at the point most distant from the neutral axis.
It may be defined as the ratio of total moment resisted by the section to the stress in the extreme fibre which is equal to yield stress.
Inelastic bending, the stress distribution in the beam is as follows:

As per the theory of pure bending :
Where M= bending moment
I = moment of inertia of the section about the bending axis.
Sigma=fibre stress at a distance ‘y’ from the centroidal/neutral axis.
R = radius of curvature of the bent beam.
E = Young’s Modulus of the material of the beam.
If y is replaced by c, the distance to remotest element, from the neutral axis or centroidal axis, then
Where Z= section modulus and is given by
This Z is the elastic section modulus used for an elastic design for the beam. It is usually denoted by Ze.
When the stress distribution in the beam becomes plastic, the analysis changes.
In the case of plastic bending:
The stress distribution within a cross-section in plastic bending is:
Moment resisted by a section that has attained full plasticity is given by:
M = Fy* (A/2) * ( Yc +Yt )
Where,
M = Moment
Fy = Yield stress
A = Area of the cross-section
Yc = distance of the centre of the area under compression from the equal-area axis.
Yt = distance of the centre of the area under tension from the equal-area axis.
Now,
M = Fy* (A/2) * ( Yc +Yt )
And,
Zp = M/Fy.
Hence,
Zp = (A/2) * ( Yc +Yt )
This is the plastic section modulus and may be used for the plastic design of beams.
For the same section, the plastic and elastic modulus are different. The difference in their values indicates the reserve in strength or moment-resisting capacity that a section made from sufficiently ductile material possesses.
The ratio between plastic and elastic section modulus is known as shape factor. The more is the value of shape factor the more is the reserve strength in the section on attaining plasticity.
Shape factor = Plastic modulus/ Elastic modulus
It can be intuitively seen that as more and more material is concentrated near the center or equal-area axis (as in circular or rhombus section) the value of shape factor increases and as more and more material is concentrated away from the center or equal area axis (as in I section) the value of shape factor decreases.
Essentials of Mechanical Stress Analysis
What is section modulus what is its significance?
Section properties: The SM of the cross-sectional shape is of significant importance in designing
How do you calculate section modulus?
The elastic section modulus is defined as S = I / y, where I is the second moment of area (or moment of inertia) and y is the distance from the neutral axis to any given fiber. It is often reported using y = c, where c is the distance from the neutral axis to the most extreme fiber, as seen in the table below.
How is section modulus used?
Section modulus is a geometric property for a given cross-section used in the design of flexural members. … You need to divide the maximum bending moment by the section modulus to get the bending stress and then compare the bending stress to the allowable tensile stress to see if the steel can take that much moment.
Conclusion:
To determine if a steel section can be curved you need to first determine its section modulus and then see if you have the correct bending equipment.
It is the direct measure of the strength of the steel. Bending a steel section that has a larger SM than another will be stronger and harder to bend.
It is a geometric property for a given cross-section used in the design of flexural members. There are two types of SM, the elastic section modulus (S) and the plastic section modulus (Z).
In the case of bending a steel section, it is important to calculate ‘S’ by taking the moment of inertia of the area of the cross-section of a structural member – divided by the distance from the neutral axis to the furthest point of the steel section.
This is where the steel will bend first. The bending moment that it takes to yield that section equals the section modulus times the yield strength.
In simple terms, it is the ratio of bending moment to bending stress for steel.
If your steel has a high (SM) it will be harder to bend and can withstand a high moment without having high bending stress.
You need to divide the maximum bending moment by the section modulus to get the bending stress and then compare the bending stress to the allowable tensile stress to see if the steel can take that much moment.
All bending equipment have SM ratings. A three-roll section bender can be designed to bend steel with section modulus between 0.4 to 500 in3.
So, to determine if the equipment can bend your steel section, you need to calculate the section modulus mathematically or by referring to engineering tables.
Then, if that amount is equal or less than that of the calculated strength of the bending machine, your machine should be able to curve the section.
What is section modulus Z?
Sectional Modulus (Z): It is the ratio of Moment of Inertia (I) of the beam cross-section about the neutral axis to the distance (ymax) of extreme fiber from the neutral axis.
What is section modulus E?
Definition. The elastic section modulus is defined as the ratio of the second moment of area (or moment of inertia) and the distance from the neutral axis to any given (or extreme) fiber. It can also be defined in terms of the first moment of area.
Is section modulus the same as Young’s modulus?
Youngs modulus is a material property, section modulus is a shape property, in other words, no relation.
What is section modulus of a fixed beam?
Section Modulus: Section modulus is defined as the ratio of moment of inertia of a beam about its C.G to the maximum distance of extreme x-section of the beam (Ymax).